一、相关定义
定义:设G = (V,E)是一个有向图,它具有下述性质:
- G中不包含有向环;
- 存在一个顶点vi,它不是任何弧的终点,而V中的其它顶点都恰好是唯一的一条弧的终点,则称 G是以vi为根的树形图。
最小树形图就是有向图G = (V, E)中以vi为根的树形图中权值和最小的那一个。
另一种说法:最小树形图,就是给有向带权图一个特殊的点root,求一棵以root为根节点的树使得该树的的总权值最小。
性质:最小树形图基于贪心和缩点的思想。
缩点:将几个点看成一个点,所有连到这几个点的边都视为连到收缩点,所有从这几个点连出的边都视为从收缩点连出
二、算法描述
【概述】
为了求一个图的最小树形图,①先求出最短弧集合E0;②如果E0不存在,则图的最小树形图也不存在;③如果E0存在且不具有环,则E0就是最小树形图;④如果E0存在但是存在有向环,则把这个环收缩成一个点u,形成新的图G1,然后对G1继续求其的最小树形图,直到求到图Gi,如果Gi不具有最小树形图,那么此图不存在最小树形图,如果Gi存在最小树形图,那么逐层展开,就得到了原图的最小树形图。
【实现细节】
设根结点为v0,
- (1)求最短弧集合E0
从所有以vi(i ≠ 0)为终点的弧中取一条最短的,若对于点i,没有入边,则不存在最小树形图,算法结束;如果能取,则得到由n个点和n-1条边组成的图G的一个子图G',这个子图的权值一定是最小的,但是不一定是一棵树。
- (2)检查E0
若E0没有有向环且不包含收缩点,则计算结束,E0就是图G以v0为根的最小树形图;若E0含有有向环,则转入步骤(3);若E0没有有向环,但是存在收缩点,转到步骤(4)。
- (3)收缩G中的有向环
把G中的环C收缩成点u,对于图G中两端都属于C的边就会被收缩掉,其他弧仍然保留,得到一个新的图G1,G1中以收缩点为终点的弧的长度要变化。变化的规则是:设点v在环C中,且环中指向v的边的权值为w,点v'不在环C中,则对于G中的每一条边<v', v>,在G1中有边<v', u>和其对应,且权值WG1(<v', u>) = WG(<v', v>) - w;对于图G中以环C中的点为起点的边<v', v>,在图G1中有边<u, v'>,则WG1(<u, v'>) = WG(<v', v>)。有一点需要注意,在这里生成的图G1可能存在重边。
对于图G和G1:
①如果图G1中没有以v0为根的最小树形图,则图G也没有;
②如果G1中有一v0为根的最小树形图,则可按照步骤(4)的展开方法得到图G的最小树形图。
所以,应该对于图G1代到(1)中反复求其最小树形图,直到G1的最小树形图u求出。
- (4)展开收缩点
假设图G1的最小树形图为T1,那么T1中所有的弧都属于图G的最小树形图T。将G1的一个收缩点u展开成环C,从C中去掉与T1具有相同终点的弧,其他弧都属于T。
【小结】
对最小树形图做个小小的总结:
1:清除自环,自环是不可能存在于任何最小树形图中的;
2:求出每个顶点的的最小入边;
3:判断该图是否存在最小树形图,由 1 可以判定,或者以图中顶点v作为根节点遍历该图就能判断是否存在最小树形图;
4:找环,之后建立新图,缩点后重新标记。
【图示——最小树形图构造流程】
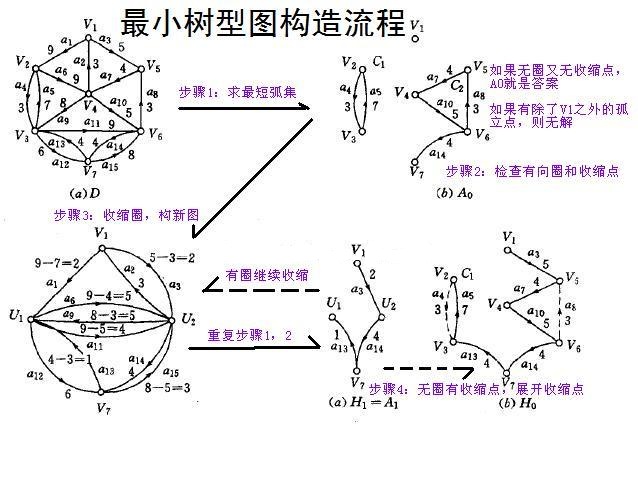
解读:第一幅图为原始图G,首先对于图G求其最短弧集合E0,即第二幅图G1;然后检查E0是满足条件,在这里,可以看到G1具有两个环,那么把这两个环收缩,如第三幅图所示,U1、U2分别为收缩后的点,然后将对应的权值进行更新,起点是环中的点,终点是环外的点,则权值不变。反之,起点是环外的点,终点是环内的点,则权值应该减去E0中指向环内点的权值,形成新的图,如第三幅图,对于其反复求最小树形图,直到不存在最小树形图,或者求得缩点后的图的最小树形图,然后展开就好了,如第六幅图。
如果只要求计算权值的话,则不需要展开,所有环中权值的和加上其他各个点与点之间,或者收缩点和点之间的权值就是总的权值。
三、沙场练兵
题目:
代码:
#includeusing namespace std;#include #include #define MAXN 1005#define INF 0x7f7f7f7ftypedef __int64 type;struct node//边的权和顶点{ int u, v; type w;}edge[MAXN * MAXN];int pre[MAXN], id[MAXN], vis[MAXN], n, m, pos;type in[MAXN];//存最小入边权,pre[v]为该边的起点type Directed_MST(int root, int V, int E){ type ret = 0;//存最小树形图总权值 while(true) { int i; //1.找每个节点的最小入边 for( i = 0; i < V; i++) in[i] = INF;//初始化为无穷大 for( i = 0; i < E; i++)//遍历每条边 { int u = edge[i].u; int v = edge[i].v; if(edge[i].w < in[v] && u != v)//说明顶点v有条权值较小的入边 记录之 { pre[v] = u;//节点u指向v in[v] = edge[i].w;//最小入边 if(u == root)//这个点就是实际的起点 pos = i; } } for( i = 0; i < V; i++)//判断是否存在最小树形图 { if(i == root) continue; if(in[i] == INF) return -1;//除了根以外有点没有入边,则根无法到达它 说明它是独立的点 一定不能构成树形图 } //2.找环 int cnt = 0;//记录环数 memset(id, -1, sizeof(id)); memset(vis, -1, sizeof(vis)); in[root] = 0; for( i = 0; i < V; i++) //标记每个环 { ret += in[i];//记录权值 int v = i; while(vis[v] != i && id[v] == -1 && v != root) { vis[v] = i; v = pre[v]; } if(v != root && id[v] == -1) { for(int u = pre[v]; u != v; u = pre[u]) id[u] = cnt;//标记节点u为第几个环 id[v] = cnt++; } } if(cnt == 0) break; //无环 则break for( i = 0; i < V; i++) if(id[i] == -1) id[i] = cnt++; //3.建立新图 缩点,重新标记 for( i = 0; i < E; i++) { int u = edge[i].u; int v = edge[i].v; edge[i].u = id[u]; edge[i].v = id[v]; if(id[u] != id[v]) edge[i].w -= in[v]; } V = cnt; root = id[root]; } return ret;}int main(){ int i; while(scanf("%d%d", &n, &m) != EOF) { type sum = 0; for( i = 0; i < m; i++) { scanf("%d%d%I64d", &edge[i].u, &edge[i].v, &edge[i].w); edge[i].u++; edge[i].v++; sum += edge[i].w; } sum ++; for( i = m; i < m + n; i++)//增加超级节点0,节点0到其余各个节点的边权相同(此题中 边权要大于原图的总边权值) { edge[i].u = 0; edge[i].v = i - m + 1; edge[i].w = sum; } type ans = Directed_MST(0, n + 1, m + n); //n+1为总结点数,m+n为总边数 //ans代表以超级节点0为根的最小树形图的总权值, //将ans减去sum,如果差值小于sum,说明节点0的出度只有1,说明原图是连通图 //如果差值>=sum,那么说明节点0的出度不止为1,说明原图不是连通图 if(ans == -1 || ans - sum >= sum) puts("impossible"); else printf("%I64d %d\n",ans - sum, pos - m); puts(""); } return 0;}